CNN

Convolutional Neural Networks

一个非常好的cnn计算过程演示网站-- https://poloclub.github.io/cnn-explainer/#article-flatten

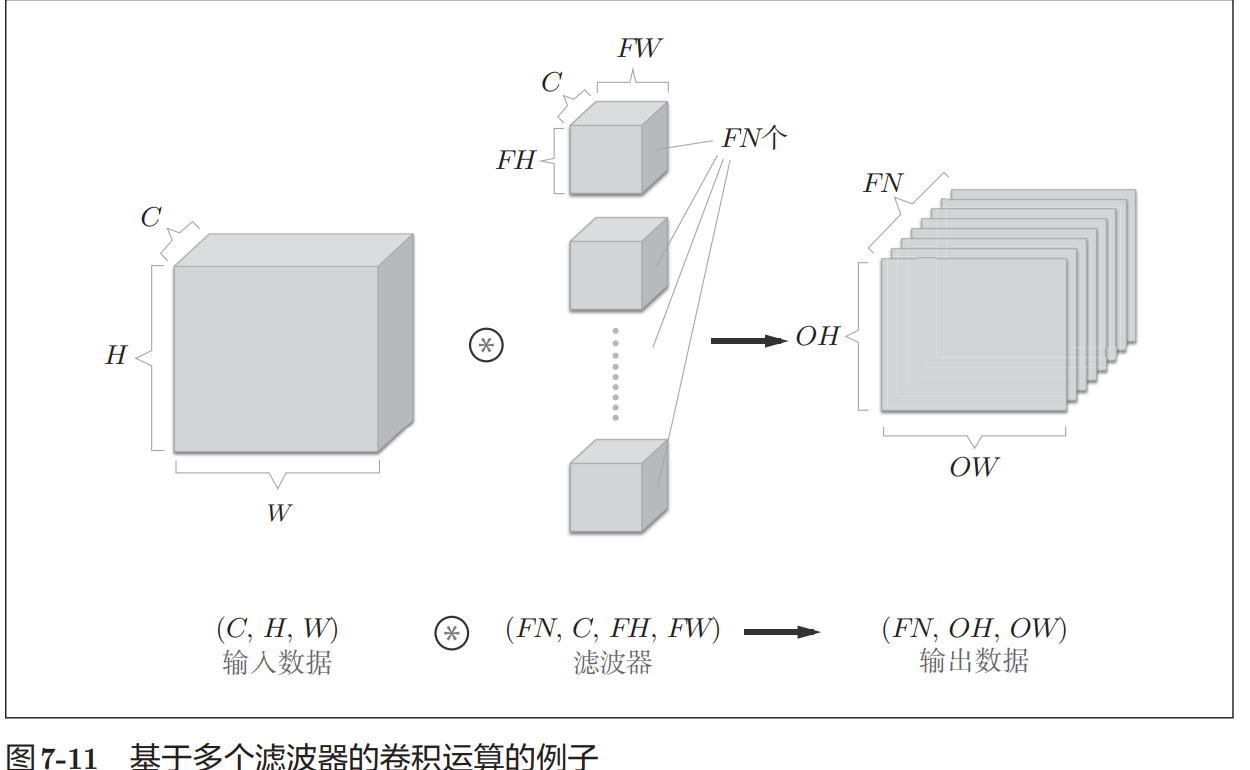
之前介绍的全连接的神经网络中使用了全连接层（Affine层）。在全连接 层中，相邻层的神经元全部连接在一起，输出的数量可以任意决定。 全连接层存在什么问题呢？那就是数据的形状被“忽视”了。比如，输 入数据是图像时，图像通常是高、长、通道方向上的3维形状。但是，向全 连接层输入时，需要将3维数据拉平为1维数据。实际上，前面提到的使用 了MNIST数据集的例子中，输入图像就是1通道、高28像素、长28像素 的（1, 28, 28）形状，但却被排成1列，以784个数据的形式输入到最开始的 Affine层。 图像是3维形状，这个形状中应该含有重要的空间信息。比如，空间上 邻近的像素为相似的值、RBG的各个通道之间分别有密切的关联性、相距 较远的像素之间没有什么关联等，3维形状中可能隐藏有值得提取的本质模 式。但是，因为全连接层会忽视形状，将全部的输入数据作为相同的神经元 （同一维度的神经元）处理，所以无法利用与形状相关的信息。 而卷积层可以保持形状不变。当输入数据是图像时，卷积层会以3维 数据的形式接收输入数据，并同样以3维数据的形式输出至下一层。因此， 在CNN中，可以（有可能）正确理解图像等具有形状的数据。

filter

• filter is a matrix of weights that are learned during the training process. ## padding
• padding is a technique used to preserve the spatial dimensions of the input volume. ## stride
• stride is the number of pixels by which we slide the filter matrix over the input volume. ## pooling
  池化是缩小高、长方向上的空间的运算。 池化层和卷积层不同，没有要学习的参数。池化只是从目标区域中取最 大值（或者平均值），所以不存在要学习的参数。
  输入数据发生微小偏差时，池化仍会返回相同的结果。因此，池化对
  输入数据的微小偏差具有鲁棒性。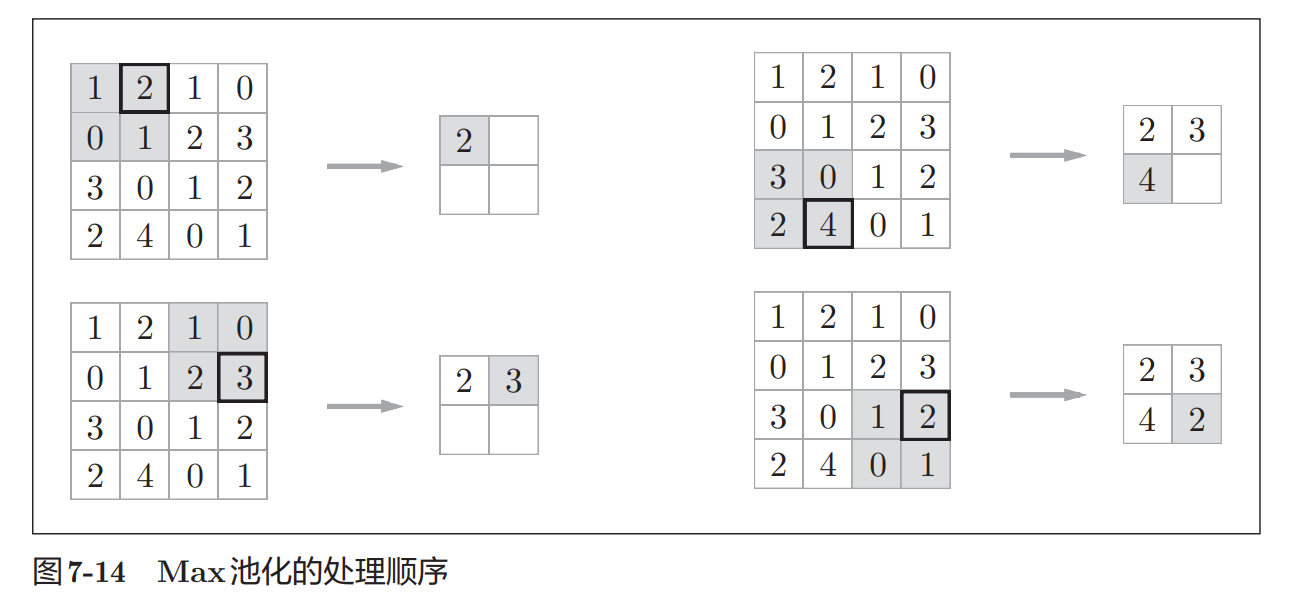

ResNet

Deep Residual Learning for Image Recognition论文精读

深度网络的学习方式

深度神经网络学习的特征可以被分为浅层/中层/深层，by

M. D. Zeiler and R. Fergus. Visualizing and understanding convolutional neural networks. In ECCV, 2014.

• 浅层学习的是图片中的边缘特征，
• 中层学习的是边缘组合形成的图形
• 深层学习的是对中层中图形的组合形成的图像

然后再通过end-to-end的方式进行分类。

所以特征的层次可以通过堆叠层数来加强。即层数越高，浅层，中层，深层学习到的东西越多。

于是产生了一个想法是层数越多，模型的学习能力越强，我们只需要设计更深的网络模型即可。

但是受到了一个障碍的限制即梯度消失/爆炸（ vanishing/exploding gradients ）

这个问题可以在一定程度上通过规则化的参数初始化和中间初始化层来解决，这使得几十层的网络的训练成为可能。

但是随着网络层数的不断提高，网络出现了退化的情况。而且这种退化不是由于过拟合引起的。

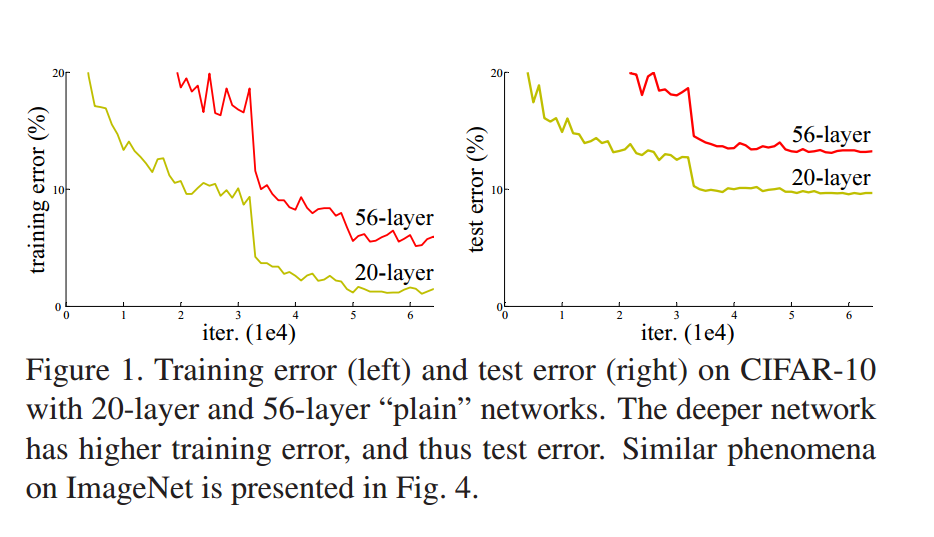
考虑一个浅层网络和一个深层网络

这个深层网络的前部与浅层网络有完全相同的结构。

思考为什么深层网络的性能会比浅层网络更差

有一种假设起码可以使深层网络具有和浅层网络具有一样的性能。

即这个深层网络的前部具有与浅层网络相同的参数，而后部可以作为一个恒等函数，这样深层网络就可以等价为与浅层网络相同的函数。

这种假设证明了深层网络不应该比浅层网络更差。但现有的手段无法实现上述假设

于是在该论文中提出了残差块这一结构来实现上述论证。

残差块

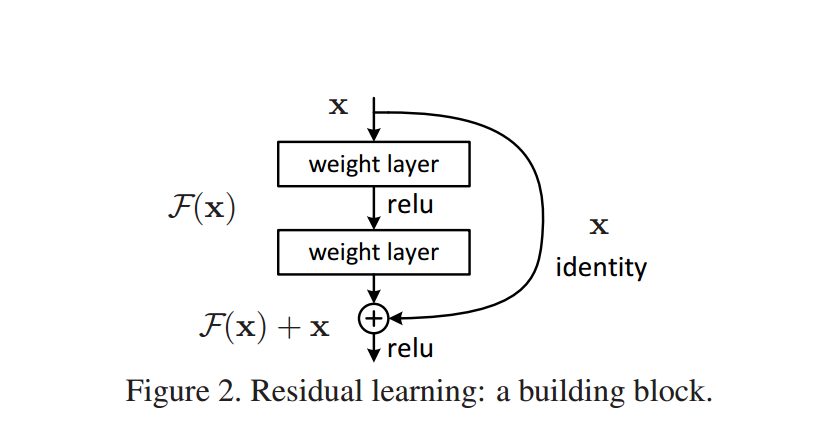
何为残差，即输出与输入的差

我们不让网络去直接拟合预期的输出，而是利用他去拟合残差

我们将期望的输出定义为 \[H(x)\]，将网络拟合的函数\[F(x)\]（残差函数）定义为：

\[ F(x) = H(x) - x \]

同时有期望输出H(x)为 \[ H(x) = F(x) + x \] 我们假定去拟合\[F(x)\]比拟合\[H(x)\]更加的容易

让我们用残差块来考虑上一节的假设，用残差块拟合成恒等函数要比一堆非线性成恒等函数要简单，也即将\[F(x)\]拟合为0比将\[H(x)\]拟合为1要容易，这也是由于初始化参数时的正负分布的特性。

这个网络是通过具有shortcut连接的前馈层来实现的，shortcut连接是指跳过一层或者多层的连接。于是shortcut连接就可以作为恒等映射（函数）。shortcut连接既不增加额外参数也不增加计算复杂度。

通过残差块我们能够构建152层的网络，并能训练成功（具有相同层数但是没有残差块的网络会在训练过程中退化），而且残差网络具能够通过提高网络的层次来提高正确率。

深度残差学习

残差块实现

\(F(x)\)和\(H(x)\)相比的优点是更容易学习。这是由于网络在向恒等学习时更加困难（网络退化现象假设表明），通过残差函数如果恒等是最优的，网络可能很容易的将权值向0移动，然后形成恒等表示，即将\[F(x)\] x向0学习，从而间接将\[H(x)\] 学习为恒等表示。实验表明，残差函数具有很小的扰动，因此恒等映射是更好的预处理。

残差块被定义为: \[ y = F(x,{W_i}) + x \] x,y是输入和输出，\[F(x,W_i)\]是需要学习的残差映射。

以图二为例，详细表示为： \[ y=W_2\sigma(W_1x + b_1)+b_2 +x \] 其中bias在图中被省略了。

\(F(x)\)的输出维数必须要和x相同，如何不是我们可以在x前乘上\[W_s\](只在匹配维度时使用)

残差函数不一定要与图二相同，可以是其他结构或层数，例如卷积层。

网络架构

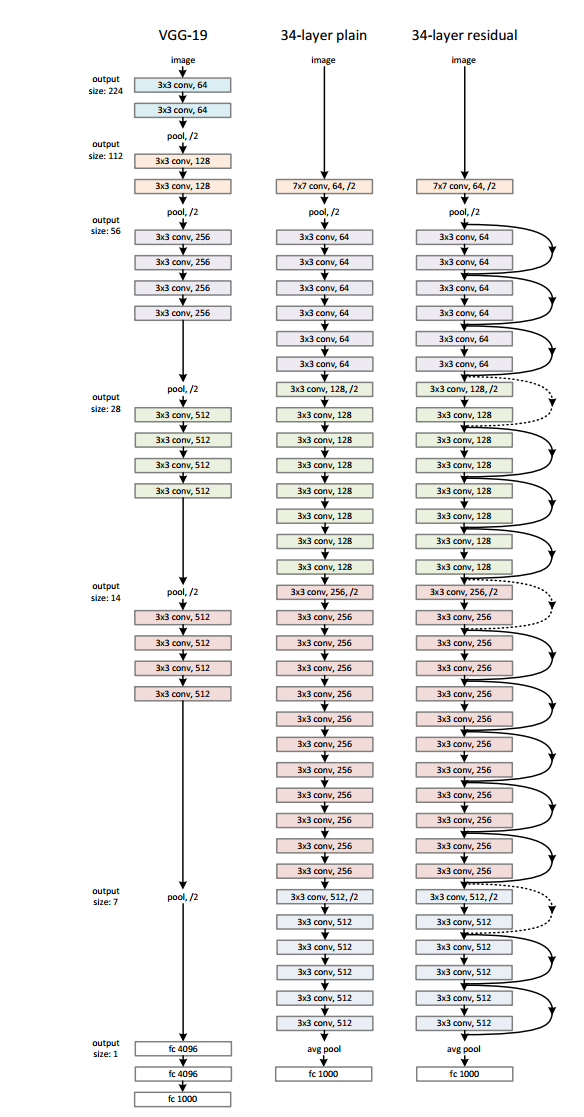
左:参考VGG-19模型(196亿FLOPs)。

中:普通网络，34个参数层(36亿FLOPs)。

右:34个参数层(36亿FLOPs)的残余网络。虚线快捷方式增加了维度。表1显示了更多细节和其他变体。

实现和虚线是shortcut连接，其中虚线代表连接的两层维数不同，采用0填充方式扩展维度。

这个网络可以说是非常的长。

普通网络

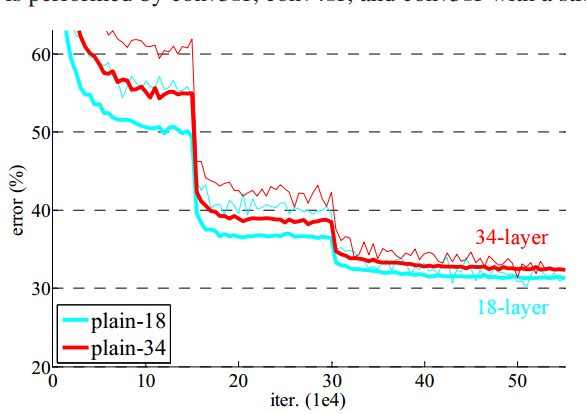
普通网络在从18层变为34层后具有更高的验证集误差，出现了退化现象。在整个训练过程中34层网络的正确率都低于18层网络

由于BN层的应用，作者推断优化消失不是由于梯度消失引起的。34层的网络依旧可以达到可观的精度（虽然比不上18层网络），作责推测是由于收敛速率降低导致的，具体原因会在后续研究（有人能告诉是哪篇文章吗）。

残差网络

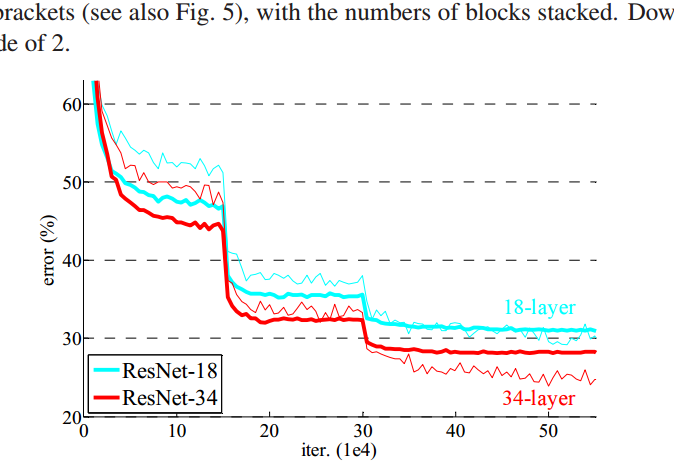
在运用了残差网络后，网络退化现象消失了，且34层网络具有更高的精度。

且在18层时与普通网络相比，收敛速度更快。

实验还研究了50/101/152层的残差网络，精度都得到了显著的提升。